The Annotated SSD with PyTorch¶
from IPython.display import Image
Image(filename='image/ssd.jpg')
Since the introduction of SSD: Single Shot Multibox Shot in 2016, it has been widely used in object detection application for its performance and speed. Using SSD, it only needs to take one shot to detect multiple objects within the image.
In this blog, I present an "annotated" version of the paper in the form of line-by-line implementation. The document itself is a working notebook, and environment to run is shared in this dockerhub repo.
Preliminary: import libraries¶
import numpy as np
import torch
import torch.nn as nn
import torch.nn.functional as F
import torchvision
import math, copy, time
from torch.autograd import Variable
import matplotlib.pyplot as plt
import seaborn
import cv2
import itertools
from utils import *
seaborn.set_context(context="talk")
%matplotlib inline
%load_ext autoreload
%autoreload 2
Table of Content¶
Background ¶
Current state of art object detection system are variants of the following approach: hypothesize bounding box, resample pixels or feature for each box, and apply a high quality classifier. This pipeline has prevailed on detection benchmarks since the selective search work through the current leading results on PASCAL VOC, COCO and ILSVRC detection all based on Faster-RCNN albert with deeper features. While accurate, these approaches have been too computationally intensive for embedded system, even with high-end hardware, too slow for real-time applications. Often detection speed for these approaches is measured in frame per second (FPS), and even the fastest high-accuracy detector, Faster-RCNN, operates at only 7 FPS. There have been many attempts to build faster detectors by attacking each stage of the detection pipeline, but so far, significantly increased speed comes only at the cost of significantly decreased detection accuracy.
This paper presents the first deep network based object detector that does not resample pixels or features for bounding box hypothese and is as accurate as approaches that do. The fundamental improvement in speed comes from eliminating bounding proposals and the subsequent pixel or feature resampling stage.
Model Architecture ¶
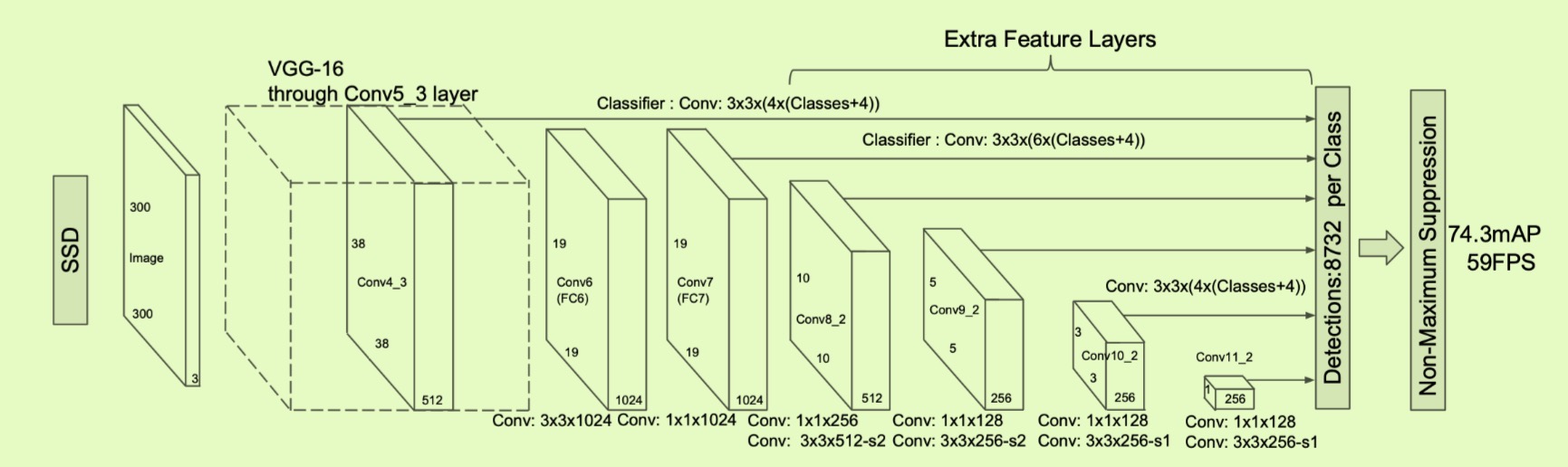
The SSD approach is based on a feed-forward convolutional network that produces a fixed-size collection of bounding boxes and scores for the presence of object class instance in those boxes, followed by a non-maximum suppresion step to produce the final detections. The early network layers are based on a standard architecture used for high quality image classification (truncated before any classification layer), which we will call base network.
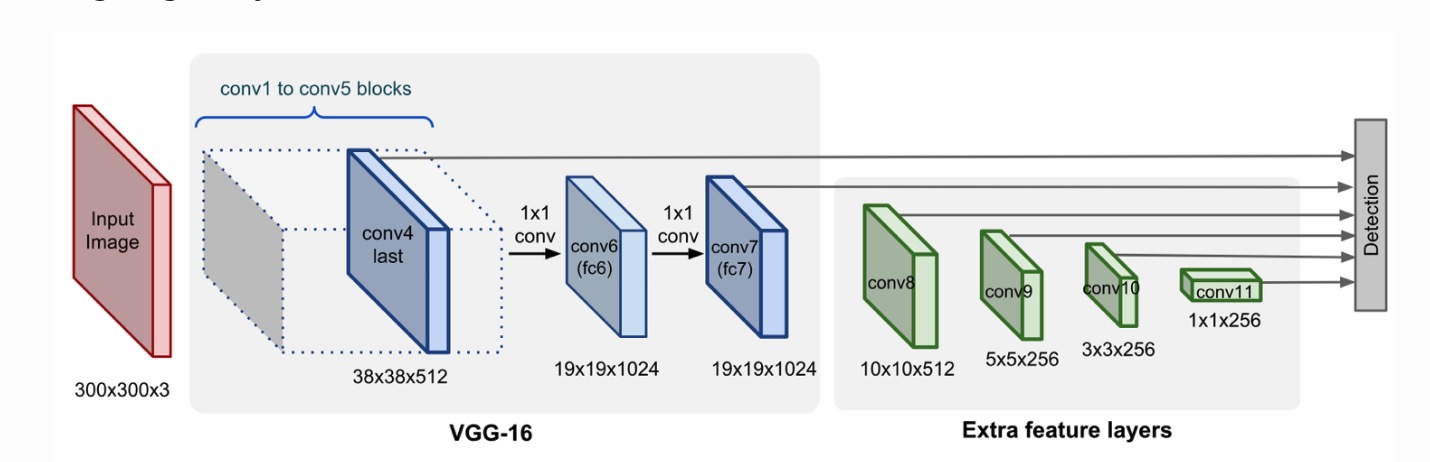
Figure.1 SSD Architecture (image from [1])
Firstly, SSD uses the VGG-16 model pre-trained on ImageNet as its base model for extracting useful image features.
original_model = torchvision.models.vgg16(pretrained=True)
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
class VGGBase(nn.Module):
"""
VGG-16 as base network
"""
def __init__(self):
super(VGGBase, self).__init__()
features = list(list(original_model.children())[:-2][0].children())[:-1]
features[16] = nn.MaxPool2d(kernel_size=2, stride=2, ceil_mode=True)
features.append(nn.MaxPool2d(kernel_size=3, stride=1, padding=1))
self.vgg_base = nn.Sequential(*features)
# replace for fc6 and fc7
self.conv6 = nn.Conv2d(512, 1024, kernel_size=3, padding=6, dilation=6)
self.conv7 = nn.Conv2d(1024, 1024, kernel_size=1)
self.load_pretrained_weights()
def forward(self, image):
"""
forward pass
:param: image: the input image
:return: layers
"""
x = image
for ii,model in enumerate(self.vgg_base):
x = model(x)
if ii in {21}:
conv4_3_feats = x
x = F.relu(self.conv6(x)) # (N, 1024, 19, 19)
conv7_feats = F.relu(self.conv7(x)) # (N, 1024, 19, 19)
return conv4_3_feats, conv7_feats
def load_pretrained_weights(self):
"""
The original VGG-16 does not contain the conv6 and con7 layers.
Therefore, we convert fc6 and fc7 into convolutional layers, and subsample by decimation. See 'decimate' in utils.py.
"""
state_dict = self.state_dict()
orignal_state_dict = original_model.state_dict()
# Convert fc6, fc7 to convolutional layers, and subsample (by decimation) to sizes of conv6 and conv7
# fc6
conv_fc6_weight = orignal_state_dict['classifier.0.weight'].view(4096, 512, 7, 7) # (4096, 512, 7, 7)
conv_fc6_bias = orignal_state_dict['classifier.0.bias'] # (4096)
state_dict['conv6.weight'] = decimate(conv_fc6_weight, m=[4, None, 3, 3]) # (1024, 512, 3, 3)
state_dict['conv6.bias'] = decimate(conv_fc6_bias, m=[4]) # (1024)
# fc7
conv_fc7_weight = orignal_state_dict['classifier.3.weight'].view(4096, 4096, 1, 1) # (4096, 4096, 1, 1)
conv_fc7_bias = orignal_state_dict['classifier.3.bias'] # (4096)
state_dict['conv7.weight'] = decimate(conv_fc7_weight, m=[4, 4, None, None]) # (1024, 1024, 1, 1)
state_dict['conv7.bias'] = decimate(conv_fc7_bias, m=[4]) # (1024)
# Note: an FC layer of size (K) operating on a flattened version (C*H*W) of a 2D image of size (C, H, W)...
# ...is equivalent to a convolutional layer with kernel size (H, W), input channels C, output channels K...
# ...operating on the 2D image of size (C, H, W) without padding
self.load_state_dict(state_dict)
Extra feature layers will be stacked on top of the base network
class ExtraConvolution(nn.Module):
"""
extra features on top of the base network
"""
def init(self):
super(ExtraConvolution,self).__init_()
self.conv8_1 = nn.Conv2d(1024, 256, kernel_size=1, padding=0)
self.conv8_2 = nn.Conv2d(256, 512, kernel_size=3, stride=2, padding=1)
self.conv9_1 = nn.Conv2d(512, 128, kernel_size=1, padding=0)
self.conv9_2 = nn.Conv2d(128, 256, kernel_size=3, stride=2, padding=1)
self.conv10_1 = nn.Conv2d(256, 128, kernel_size=1, padding=0)
self.conv10_2 = nn.Conv2d(128, 256, kernel_size=3, padding=0)
self.conv11_1 = nn.Conv2d(256, 128, kernel_size=1, padding=0)
self.conv11_2 = nn.Conv2d(128, 256, kernel_size=3, padding=0)
def forward(self, conv7_feats):
"""
Forward propagation.
:param conv7_feats: lower-level conv7 feature map, a tensor of dimensions (N, 1024, 19, 19)
:return: higher-level feature maps conv8_2, conv9_2, conv10_2, and conv11_2
"""
out = F.relu(self.conv8_1(conv7_feats)) # (N, 256, 19, 19)
out = F.relu(self.conv8_2(out)) # (N, 512, 10, 10)
conv8_2_feats = out # (N, 512, 10, 10)
out = F.relu(self.conv9_1(out)) # (N, 128, 10, 10)
out = F.relu(self.conv9_2(out)) # (N, 256, 5, 5)
conv9_2_feats = out # (N, 256, 5, 5)
out = F.relu(self.conv10_1(out)) # (N, 128, 5, 5)
out = F.relu(self.conv10_2(out)) # (N, 256, 3, 3)
conv10_2_feats = out # (N, 256, 3, 3)
out = F.relu(self.conv11_1(out)) # (N, 128, 3, 3)
conv11_2_feats = F.relu(self.conv11_2(out)) # (N, 256, 1, 1)
# Higher-level feature maps
return conv8_2_feats, conv9_2_feats, conv10_2_feats, conv11_2_feats
Convolutional predictors for detection ¶
For each default box of each cell at feature map, we want to predict
- the offsets relative to the default box shapes in the cell
- the per-class scores that indicate the presence of a class instance in each of those boxes.
class ConvPredictor(nn.Module):
"""
Predict per-class score and bounding boxes using feature maps
"""
def __init__(self, n_classes):
"""
Param:
n_classes : number of different types of objects
"""
super(ConvPredictor, self).__init__()
self.n_classes = n_classes
# number of default boxes per cell in feature map
default_boxes = {
'conv4_3' : 4,
'conv7' : 6,
'conv8_2' : 6,
'conv9_2' : 6,
'conv10_2' : 4,
'conv11_2' : 4
}
# predict offset for each default box
self.loc_conv4_3 = nn.Conv2d(512, default_boxes['conv4_3']*4, kernel_size=3, padding=1)
self.loc_conv7 = nn.Conv2d(1024, default_boxes['conv7']*4, kernel_size=3, padding=1)
self.loc_conv8_2 = nn.Conv2d(512, default_boxes['conv8_2']*4, kernel_size=3, padding=1)
self.loc_conv9_2 = nn.Conv2d(256, default_boxes['conv9_2']*4, kernel_size=3, padding=1)
self.loc_conv10_2 = nn.Conv2d(256, default_boxes['conv10_2']*4, kernel_size=3, padding=1)
self.loc_conv11_2 = nn.Conv2d(256, default_boxes['conv11_2']*4, kernel_size=3, padding=1)
# predict per-class score
self.cls_conv4_3 = nn.Conv2d(512, default_boxes['conv4_3']*n_classes, kernel_size=3, padding=1)
self.cls_conv7 = nn.Conv2d(1024, default_boxes['conv7']*n_classes, kernel_size=3, padding=1)
self.cls_conv8_2 = nn.Conv2d(512, default_boxes['conv8_2']*n_classes, kernel_size=3, padding=1)
self.cls_conv9_2 = nn.Conv2d(256, default_boxes['conv9_2']*n_classes, kernel_size=3, padding=1)
self.cls_conv10_2 = nn.Conv2d(256, default_boxes['conv10_2']*n_classes, kernel_size=3, padding=1)
self.cls_conv11_2 = nn.Conv2d(256, default_boxes['conv11_2']*n_classes, kernel_size=3, padding=1)
def forward(self, conv4_3_features, conv7_features, conv8_2_features, conv9_2_features, conv10_2_features, conv11_2_featurs):
"""
Feed forward propagation
Params:
conv4_3_features: feature map from conv4_3 of dimension (N, 512, 38, 38)
conv7_features: feature map from conv7 of dimension (N, 1024, 19, 19)
conv8_2_features: feature map from conv8_2 of dimension (N, 512, 10, 10)
conv9_2_features: feature map from conv9_2 of dimension (N, 256, 5, 5)
conv10_2_features: feature map from conv10_2 of dimension (N, 256, 3, 3)
conv11_2_features: feature map from conv11_2 of dimension (N, 256, 1, 1)
Return:
loc_offs: location offsets for 8732 default boxes
class_scores: class scores for 8732*n_classes
"""
batch_size = conv4_3_features.size(0)
loc_off_conv4_3 = self.loc_conv4_3(conv4_3_features)
loc_off_conv4_3 = loc_off_conv4_3.permute(0,2,3,1).contiguous()
loc_off_conv4_3 = loc_off_conv4_3.view(batch_size, -1, 4)
loc_off_conv7 = self.loc_conv7(conv7_features)
loc_off_conv7 = loc_off_conv7.permuate(0,2,3,1).contiguous()
loc_off_conv7 = loc_off_conv7.view(batch_size, -1, 4)
loc_off_conv8_2 = self.loc_conv8_2(conv8_2_features)
loc_off_conv8_2 = loc_off_conv8_2.permute(0,2,3,1).contiguous()
loc_off_conv8_2 = loc_off_conv8_2.view(batch_size, -1, 4)
loc_off_conv9_2 = self.loc_off_conv9_2(conv9_2_features)
loc_off_conv9_2 = loc_off_conv9_2.permuate(0,2,3,1).contiguous()
loc_off_conv9_2 = loc_off_conv9_2.view(batch_size, -1, 4)
loc_off_conv10_2 = self.loc_off_conv10_2(conv10_2_features)
loc_off_conv10_2 = loc_off_conv10_2.permuate(0,2,3,1).contiguous()
loc_off_conv10_2 = loc_off_conv10_2.view(batch_size, -1, 4)
loc_off_conv11_2 = self.loc_conv11_2(conv11_2_featurs)
loc_off_conv11_2 = loc_off_conv11_2.permute(0,2,3,1).contiguous()
loc_off_conv11_2 = loc_off_conv11_2.view(batch_size, -1, 4)
# predict per-class score for each default boxes
cls_conv4_3 = self.cls_conv4_3(conv4_3_features)
cls_conv4_3 = cls_conv4_3.permute(0,2,3,1).contiguous()
cls_conv4_3 = cls_conv4_3.view(batch_size,-1, self.n_classes)
cls_conv7 = self.cls_conv7(conv7_features)
cls_conv7 = cls_conv7.permuate(0,2,3,1).contiguous()
cls_conv7 = cls_conv7.view(batch_size,-1, self.n_classes)
cls_conv8_2 = self.cls_conv8_2(conv8_2_features)
cls_conv8_2 = cls_conv8_2.permute(0,2,3,1).contiguous()
cls_conv8_2 = cls_conv8_2.view(batch_size,-1,self.n_classes)
cls_conv9_2 = self.cls_conv9_2(conv9_2_features)
cls_conv9_2 = cls_conv9_2.permute(0,2,3,1).contiguous()
cls_conv9_2 = cls_conv9_2.view(batch_size, -1, self.n_classes)
cls_conv10_2 = self.cls_conv10_2(conv10_2_features)
cls_conv10_2 = cls_conv10_2.permute(0,2,3,1).contiguous()
cls_conv10_2 = cls_conv10_2.view(batch_size,-1,self.n_classes)
cls_conv11_2 = self.cls_conv11_2(conv11_2_featurs)
cls_conv11_2 = cls_conv11_2.permute(0,2,3,1).contiguous()
cls_conv11_2 = cls_conv11_2.view(batch_size,-1,self.n_classes)
loc_offs = torch.cat([loc_off_conv4_3, loc_off_conv7, loc_off_conv8_2, loc_off_conv9_2, loc_off_conv10_2, loc_off_conv11_2], dim=1)
class_scores = torch.cat([cls_conv4_3, cls_conv7, cls_conv8_2, cls_conv9_2, cls_conv10_2, cls_conv11_2], dim=1)
return loc_offs, class_scores
SSD300 model ¶
Default boxes ¶
SSD predicts offset of predefined default boxes for every location of the feature maps. The default boxes are manually chosen based on the shapes and size of labelled object in target dataset.
How to choose scale and aspect ratio for the default box? Feature maps from different levels within a network are known to have different receptive field sizes. Fortunately, within the SSD framework, the default boxes do not necessary need to correspond to the actual receptive fields of each layer. The paper designs the tiling the default boxes so that specific feature maps learn to be responsive to particular scales of the objects.
Scale¶
Suppose we want to use m feature maps for prediction, The scale of the default boxes for each feature is computed as:
$$s_k = s_{min}+\frac{s_{max}-s_{min}}{m-1}(k-1), k \in[1,m]$$where $s_{min}$ is 0.2 and $s_{max}$ is 0.9, meaning the lowest layer has a scale of 0.2 and the highest layer has a scale of 0.9, and all layers in between are regularly spaced.
Aspect Ratio¶
The paper imposes different aspect ratio for the default boxes, denote them as $a_r \in \{1,2,3,\frac{1}{2}, \frac{1}{3}\}$. The width of default box is $w_{k}^a = s_k\sqrt{a_r}$ and height $h_{k}^a = s_k/\sqrt{a_r}$. For the aspect ratio of 1, the paper also add a default box whose scale is $s_k^{'} = \sqrt{s_ks_{k+1}}$, resulting in 6 default boxes per feature map location.
Center¶
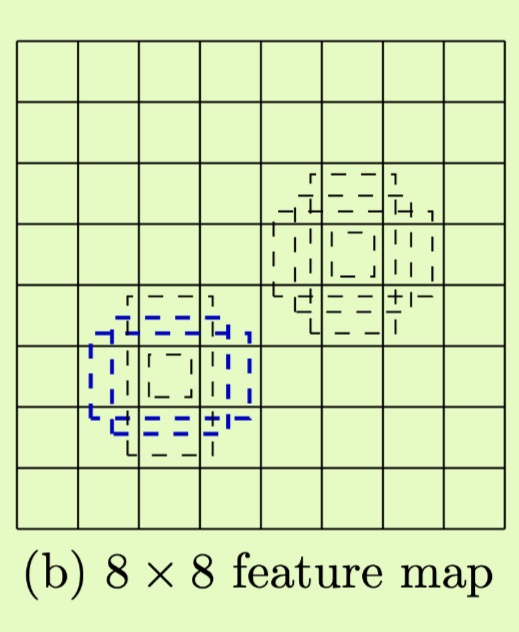
The paper set the center of each default box to $(\frac{i+0.5}{|f_k|},\frac{j+0.5}{|f_k|})$, where $|f_k|$ is the size of the k-th square feature map, $i,j \in [0, |f_k|]$
The default boxes as shown in the figure. Note: here there are 4 boxes (with aspect ratio ${1,2,\frac{1}{2}}$)
SSD300 Implementation Details¶
Default boxes¶
- The paper sets default box with scale 0.1 on conv4_3.
- For conv4_3, conv10_2 and conv11_2, the paper only associates 4 default boxes at each feature map location - omitting aspect ratio of $\frac{1}{3}$ and 3.
- For all other layers, the paper put 6 default boxes
Post-processing of predictions¶
def create_default_boxes():
"""
create 8732 default boxes for SSD300
Return:
default boxes of dimension (8732,4)
"""
feature_map_dims = {
'conv4_3' : 38,
'conv7' : 19,
'conv8_2' : 10,
'conv9_2' : 5,
'conv10_2' : 3,
'conv11_2' : 1
}
box_scale = {
'conv4_3' : 0.1,
'conv7' : 0.26,
'conv8_2':0.42,
'conv9_2':0.58,
'conv10_2' : 0.74,
'conv11_2' : 0.9
}
box_aspect_ratios = {
'conv4_3': [1, 2, 0.5],
'conv7':[1,2,3,0.5,0.33],
'conv8_2':[1,2,3,0.5,0.33],
'conv9_2':[1,2,3,0.5,0.33],
'conv10_2':[1,2,0.5],
'conv11_2':[1,2,0.5]
}
feature_map_names = list(feature_map_dims.keys())
default_boxes = []
for k, fmap_name in enumerate(feature_map_names):
for i, j in itertools.product(range(feature_map_dims[fmap_name]), repeat=2):
center_x = (j+0.5)/feature_map_dims[fmap_name]
center_y = (i+0.5)/feature_map_dims[fmap_name]
for ratio in box_aspect_ratios[fmap_name]:
default_boxes.append([center_x, center_y, box_scale[fmap_name]*np.sqrt(ratio), box_scale[fmap_name]/np.sqrt(ratio)])
if ratio == 1:
if k == len(feature_map_names)-1:
additional_scale = 1
else:
additional_scale = np.sqrt(box_scale[fmap_name]*box_scale[feature_map_names[k+1]])
default_boxes.append([center_x, center_y, additional_scale, additional_scale])
default_boxes = torch.FloatTensor(default_boxes)
default_boxes.clamp_(0,1)
return default_boxes
class SSD300(nn.Module):
"""
SSD300 model which includes base network, extra convolution layers and prediction convolutions
"""
def __init__(self, n_classes):
super(SSD300, self).__init__()
self.n_classes = n_classes
self.base = VGGBase()
self.extra_conv = ExtraConvolution()
self.conv_predictor = ConvPredictor(n_classes)
# conv4_ has a different feature scale compared to the other layers, the paper uses
# the L2 normalization technique to scale the feature norm at each location in the
# feature map to 20 and learn the scale during propagation.
self.scale_factor = nn.Parameter(torch.FloatTensor(1,512,1,1))
nn.init.constant_(self.scale_factor, 20)
# generate default boxes
self.default_box_coordinates = create_default_boxes()
def forward(self, image):
"""
Forward propagation for ssd300
Params:
image: a tensor of dimension (N,3,300,300)
Return:
loc_offs: location offsets for 8732 default boxes
class_scores: class scores for 8732*n_classes
"""
# lower feature maps from vgg base network, conv4_3 and conv7
conv4_3_features, conv7_features = self.base(image)
## rescale conv4_3
l2_norm = conv4_3_features.pow(2).sum(dim=1, keepdim=True).sqrt()
conv4_3_features = conv4_3_features/l2_norm
conv4_3_features = conv4_3_features*self.scale_factor
# higher feature maps from extra convolution layer, conv8_2, conv9_2, conv10_2, conv11_2
conv8_2_features, conv9_2_features, conv10_2_features, conv11_2_features = self.extra_conv(conv7_features)
# run convolutional prediction
loc_offs, class_scores = self.conv_predictor(conv4_3_features, conv7_features, conv8_2_features, conv9_2_features, conv10_2_features, conv11_2_features)
return loc_offs, class_scores
def detect_objects(self, predicted_loc_offs, predicted_scores, min_score, max_overlap, top_k):
"""
Post processing of the detection boxes and score from SSD300
Params:
predicted_loc_offs: predicted location offsets with the default boxes
predicted_scores: predicted class scores
min_score: minimum threshold for a detected box to be consider as a object
max_overlap: maximum overlap of two detected boxes can have so that the lower scored box not be suppressed
top_k : keep only the top k detecttion across all classes
"""
batch_size = predicted_loc_offs.size(0)
num_default_boxes = self.default_box_coordinates.size(0)
predicted_scores = F.softmax(predicted_scores, dim=2)
# list to store the detected boxes, labels and scores for batch images
batch_image_boxes = list()
batch_image_labels = list()
batch_image_scores = list()
assert num_default_boxes == predicted_loc_offs.size(1) == predicted_scores.size(1)
for image_index in range(batch_size):
predicted_boxes = centerxy_to_xy(offxy_to_centerxy(predicted_loc_offs[image_index], self.default_box_coordinates))
max_score, class_label = predicted_scores[image_index].max(dim=1)
image_boxes = list()
image_labels = list()
image_scores = list()
# iterate through all classes
for cls in range(1, self.n_classes):
cls_scores = predicted_scores[image_index][:,cls]
score_above_min = cls_scores > min_score
num_score_above_min = score_above_min.sum().item()
# if there is no score over the min score for the class
if num_score_above_min == 0:
continue
cls_scores = cls_scores[score_above_min] # only the score adove min_score
cls_predicted_boxes = predicted_boxes[score_above_min] # the box coordinates for the corresponding score over min_score
# sort the class score and predicted boxes
cls_scores, sort_ind = cls_scores.sort(dim=0, descending=True)
cls_predicted_boxes = predicted_boxes[sort_ind]
# calculate the IoU from two box sets, that is to find the IoU among all the predicted boxes
ious = calculate_IoU(cls_predicted_boxes, cls_predicted_boxes)
# Non Maxisum Suppresion, a torch.uint8 tensor to keep track of which boxes are suppressed
# 1 : suppressed, 0: keep
suppress = torch.zeros((num_score_above_min),dtype=torch.uint8).to(device)
for box_index in range(num_score_above_min):
if suppress[box_index] == 1:
continue
suppress = torch.max(suppress, ious[box_index]>max_overlap)
suppress[box_index] = 0
# store unsuppressed boxes, labels and scores
image_boxes.append(cls_predicted_boxes[1-suppress])
image_labels.append(torch.LongTensor(1-suppress).sum().item()*[cls].to(device))
image_scores.append(cls_scores[1-suppress])
# if no object in the image is found, add a background class
if len(image_boxes) == 0:
image_boxes.append(torch.FloatTensor([0.,0.,1.,1.])).to(device)
image_labels.append(torch.LongTensor([0])).to(device)
image_scores.append(torch.FloatTensor([0.])).to(device)
# concatnate to single output for single image
image_boxes = torch.cat(image_boxes, dim=0)
image_labels = torch.cat(image_labels, dim=0)
image_scores = torch.cat(image_scores, dim=0)
n_object = image_score.size(0)
if n_object > top_k:
image_scores, sorted_index = image_scores.sort(dim=0, descending=True)
image_scores = image_scores[:top_k]
image_labels = image_labels[sorted_index][:top_k]
image_boxes = image_boxes[sorted_index][:top_k]
batch_image_boxes.append(image_boxes)
batch_image_scores.append(image_scores)
batch_image_labels.append(image_labels)
return batch_image_boxes, batch_image_labels, batch_image_scores
Training ¶
Matching Strategy¶
During training, it needs to match which default boxes correspond to a ground truth detection and train the network accordingly. For each ground truth box we are selecting from default boxes that vary over location, aspect ratio and scale. The paper matches default boxes to any ground truth box with IoU higher than a threshold (0.5).
Training Objective¶
The overall objective loss function is a weighted sum of the localization loss (loc) and the confidence loss (conf): $$L(x,c,l,g)=\frac{1}{N}(L_{conf}(x,c)+\alpha L_{loc}(x,l,g))$$ where N is the number of matched default boxes, if $N=0$, we set the loss to 0.
The localization loss is a Smooth L1 loss between prediction box ($l$) and ground truth box ($g$). Similar to Faster-RCNN, the paper regress to offsets for the center (cx, cy) of the defualt box ($d$) and for its height ($h$) and width ($w$). Based on the matching strategy, let $x_{i,j}^p=\{1,0\}$ be an indicator for matching the $i$th default box to $j$th ground truth box of category $p$. $$L_{loc}(x, l, g) = \sum^N_{i\in Pos}\sum_{m \in \{cx, cy, w, h\}}x_{i,j}^{k} smooth_{L1}(l_i^m-\hat{g}_j^m)$$ $$\hat{g}_j^{cx}=(g_j^{cx}-d_i^{cx})/d_i^{w}$$ $$\hat{g}_j^{cy}=(g_j^{cy}-d_i^{cy})/d_i^{h}$$ $$\hat{g}_j^w =log(\frac{g_j^w}{d_i^w})$$ $$\hat{g}_j^h =log(\frac{g_j^h}{d_i^h})$$
The confidence loss is the softmax loss over multiple classes confidence (c). $$L_{conf}(x,c)=-\sum_{i \in Pos}^N x_{i,j}^p log(\hat{c}_i^p)-\sum_{i \in Neg}^N log(\hat{c}_i^0)$$ where $\hat{c}_i^p=\frac{exp(c_i^p)}{\sum_p exp(c_i^p)}$
Hard Negative Mining¶
After the matching step, most of the default boxes are negtive, especially when the number of possible default boxes is large. This introduces a significant imbalance between the positive and negative training examples. Instead using all the negative samples, we sort them by using the highest confidence for each default box and pick the top ones so that the ratio between the negative and positive is at most 3:1.
class MultiboxLoss(nn.Module):
"""
The multibox loss for the location loss and confidence loss
"""
def __init__(self, default_center_xy, threshold=0.5, neg_pos_ratio=3, alpha=1.):
super(MultiboxLoss, self).__init__()
self.default_center_xy = default_center_xy
self.default_xy = centerxy_to_xy(self.default_center_xy)
self.threshold = threshold
self.neg_pos_ratio = neg_pos_ratio
self.alpha = alpha
self.smooth_l1 = nn.L1Loss()
self.cross_entropy = nn.CrossEntropyLoss(reduce=False)
def forward(self, predicted_loc_offs, predicted_scores, boxes, labels):
"""
Calculate the multibox loss
Params:
predicted_loc_offs: the predicted bounding box offset for the default boxes
predicted_scores: confidence level for each the bounding box
boxes: ground truth bounding box
labels: grounth truth label for the groud truth bounding box
"""
batch_size = predicted_loc_offs.size(0)
num_default_boxes = self.default_center_xy.size(0)
num_classes = predicted_scores.size(2)
true_loc_offs = torch.zeros((batch_size, num_default_boxe, 4), dtype=torch.float).to(device)
true_classes = torch.zeros((batch_size, num_default_boxes), dtype=torch.long).to(device)
for ind in range(batch_size):
num_objects = boxes[ind].size(0)
ious = calculate_IoU(boxes[ind], self.default_xy)
# for each default box, get the object with max iou
iou_for_default, obj_for_default = ious.max(dim=0)
# get the default box for the object with max iou
_, default_for_obj = iou.max(dim=1)
obj_for_default[default_for_obj] = torch.LongTensor(range(num_objects)).to(device)
iou_for_default[default_for_obj] = 1
# label for each prior
label_for_default = labels[i][obj_for_default]
label_for_default[iou_for_default<self.threshold]=0
true_classes = label_for_default
true_loc_offs = centerxy_to_off(xy_to_centerxy(boxes[i][obj_for_default]), self.default_center_xy)
# localization loss, L1 loss
foreground_default = true_classes != 0
localization_loss = self.smooth_l1(predicted_loc_offs[foreground_default], true_loc_offs[foreground_default])
# confidence loss
num_foreground = foreground_default.sum(dim=1)
num_hard_negative = self.neg_pos_ratio*num_foreground
cross_entropy_loss = self.cross_entropy(predicted_scores.view(-1, num_classes), true_classes.view(-1)).view(batch_size, num_default_boxes)
# the default box for positive
cross_entropy_loss_pos = cross_entropy_loss[foreground_default]
cross_entropy_loss_neg = cross_entropy_loss.clone()
cross_entropy_loss_neg[foreground_default] = 0
cross_entropy_loss_neg, _ = cross_entropy_loss_neg.sort(dim=1, descending=True)
hard_negative_rank = torch.LongTensor(range(num_default_boxes)).unsqueeze(0).expand_as(cross_entropy_loss_neg)
hard_negative_ind = hard_negative_rank < num_hard_negative.unsqueeze(0)
cross_entropy_loss_hard_neg = cross_entropy_loss_neg[hard_negative_ind]
cross_entropy_loss = (cross_entropy_loss_hard_neg.sum()+cross_entropy_loss_pos.sum())/num_foreground().float()
return cross_entropy_loss+self.alpha*localization_loss
Conclusion ¶
The paper introduce SSD, a fast single-shot object detector for multiple categories. A key feature of the model is the use of multi-scale convoluational bounding box outputs attached to multiple feature maps at the top of the network. This representation allows to efficiently model the spaces of possible box shapes.